How to check if page mode is Experience Forms

In this post I share a quick tip on how to to check if the current page is Forms Designer.
Sitecore Forms comes with default form elements that you can easily drag and drop on your form. Those default form elements are divided into four categories: Basic, Lists, Security, and Structure. They contain mostly of the fields you are going to need such as Text Fields, Checkboxes, Lists, Password, Emails, and other. But, at some point you will need to create a custom form elements to meet your client’s requirement.
Why would you want to check if the current page is Forms Designer?
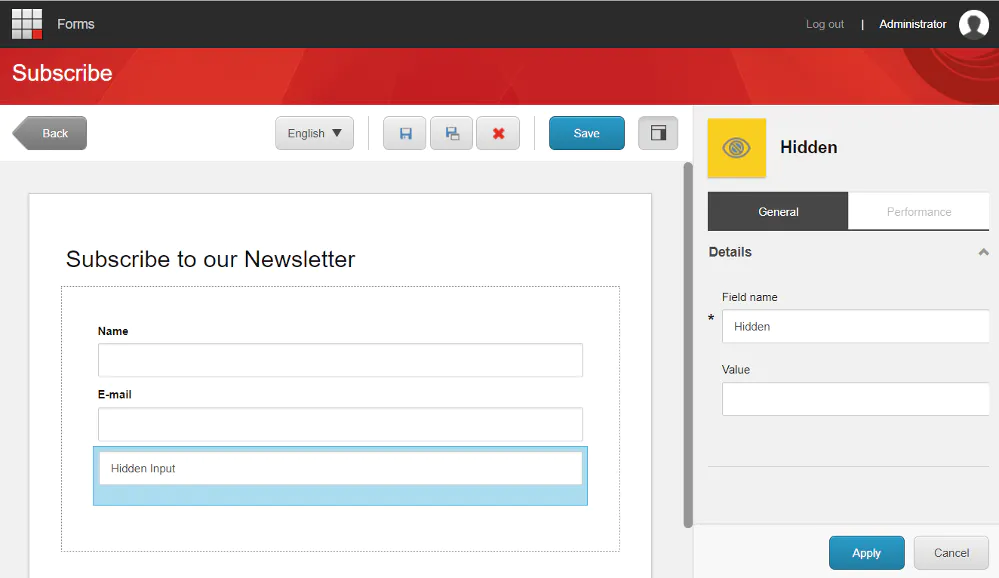
Sometimes, you might want that a custom form element holds certain values but not necessarily show them to a visitor. e.g. a HTML hidden field.
As you can see in the image above, the forms editing experience is compromised with an field that is barely visible for the form editor.
If you try to use properties such as Sitecore.Context.PageMode.IsExperienceEditor or Sitecore.Context.PageMode.IsNormal, none of them assert that the current page is Forms Designer. Actually, when you are in Forms Designer page, Sitecore.Context.PageMode.IsNormal has the value of true.
How do you check if the current page is Form Designer?
Whenever you are in the Form Designer page, you will notice that the url has a query string parameter named sc_formmode. That is the one we are going to use in order to check if the current page is Form Designer.
Let’s create an extension method to check if the current page is Form Designer.
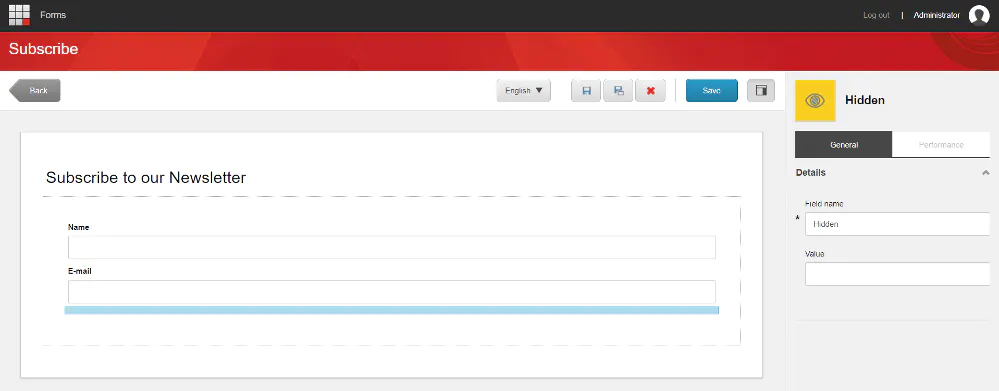
Then finally, we use this extension method to render a better experience for the form editor.